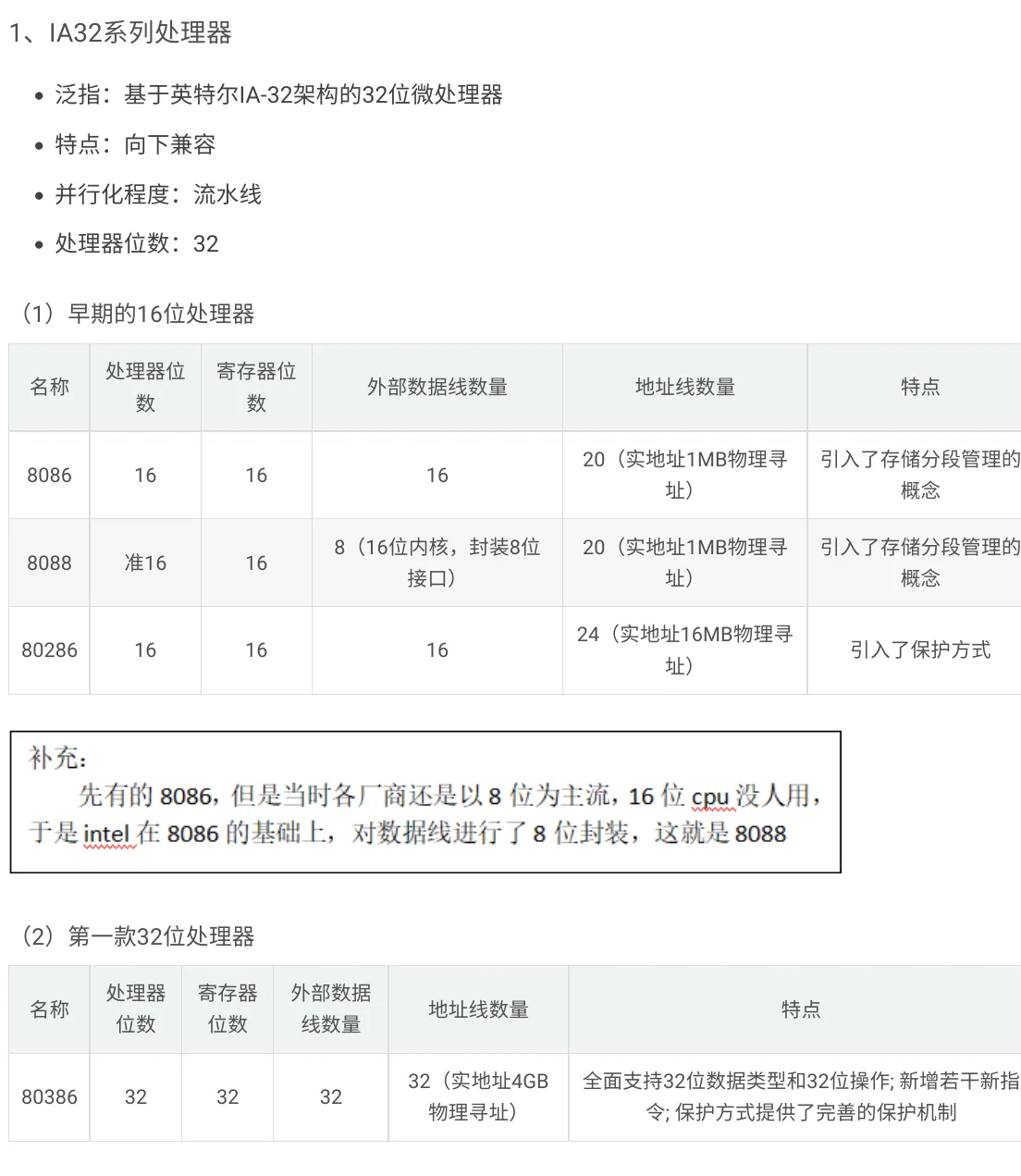
0-LL文法
pridelizihaoLL文法的两个函数
FIRST AND FOLLOW
- 花了很长时间,终于搞明白了LL文法的FIRST和FOLLOW相关的内容,希望对大家有所帮助
FIRST
- 对于FIRST(α)我们看产生式头可以推导得到的产生式体中的首个符号集合,即计算FIRST时非终结符号处于产生式的头部。
定义
FIRST(a)被定义为可以从a推导得到的串的首符号的集合,其中a是任意的文法符号串
FIRST(a)={a=>*b…,b是终结符}
如果a=>*e,e也属于FIRST(a)
计算方法
如果X是终结符,那么FIRST(X)=X
如果X->Y1Y2Y3…Yk,且a在FIRST(Yi)中,且Y1=>*e,Y2=>*e,…,Yi-1=>*e,那么a在FIRST(X)中
如果X->e,那么e在FIRST(X)中
例子
FOLLOW
- 计算FOLLOW时非终结符号位于产生式体中,查看当前产生式体中(或者叫句型的右边部分)非终结符号紧挨着的 终结符号 集合。
定义
FOLLOW(A)被定义为可能紧跟在A右边的终极符的集合
FOLLOW(A)={a,S=>*…Aa…,a是终结符}
如果说A是某个句型的最右符号,那么$属于FOLLOW(A)
计算方法
将$放到FOLLOW(S)中,S是开始符号,$是输入右端的结束标志
如果存在A->aBC,那么FIRST(C)中非空的符号都在FOLLOW(B)中
如果存在A->aB,或A->aBC且FIRST(C)中包含e,则FOLLOW(A)中的所有符号都在FOLLOW(B)中
实例
根据文法推FIRST和FOLLOW
实例1
实例2
我们对下面文法来求解FIRST和FOLLOW集合:
E→TE′
E′→+TE′ | ϵ
T→FT′
T′→∗FT′ | ϵ
F→(E) | id
首先我们以非终结符号出现的顺序,将它们按照顺序排列起来(有点像消除左递归时,我们创建的非终结符号集合): E, T, E′, F, T′
1)、 非终结符号E :
FIRST(E) = { ( , id },其推导过程为: E⇒TE′⇒FT′E′⇒(E)T′E′ | idT′E′;
FOLLOW(E) = { ), $ }。从产生式 F→(E) 我们可以得到一个终结符号。而且从求FOLLOW的第一点可知,对于开始符号,我们需要将$添加进去。
2)、 非终结符号E’:
FIRST(E’) = { +, ε },其推导过程为:E′→+TE′ | ϵ。
FOLLOW(E’) = { ), $ },这是因为产生式 E→TE′ 可知,FOLLOW(E)和FOLLOW(E’)是完全等价的。
3)、 非终结符号T: FIRST(T) = { ( , id },其推导过程为: T⇒FT′⇒(E)T′E′ | idT′E′
FOLLOW(T)的计算从上述的文法中可以看出,非终结符号T出现在产生式体中的有 TE′, +TE′ ,也就是在其后面的均为非终结符号E’。因此FOLLOW(T)包含FIRST(E’);
由于E’可以推导出空串ε,而且根据产生式 E→TE′。我们可以知道FOLLOW(T)同样等于FOLLOW(E)。因此求出上面两个的并集为:
FOLLOW(T) = { +, ), $ }。
4)、 非终结符号T‘: FIRST(T’) = { * ,ε },其推导过程为:T′→∗FT′ | ϵ;
FOLLOW(T’) = { +, ), $ }。这是因为根据产生式 T→FT′ 可知,FOLLOW(T’)和FOLLOW(T)是相同的;
5)、 非终结符号F: FIRST(F) = { (, id },其推导过程为 F→(E) | id;
FOLLOW(F)的计算和非终结符号T是类似的,首先我们根据产生式 T→FT′, T′→∗FT′可知,非终结符号F其后紧跟着非终结符号T’,因此FOLLOW(F)则包含了FIRST(T’);
而且我们从产生式 T→FT′, T′→∗FT′ | ϵ 可知,T’可以推导出空串ε,因此FOLLOW(F)也包含有FOLLOW(T);
因此最终的结论为:FOLLOW(F) = { *, +, ), $ }
判断是否为LL(1)文法
LL(1)中的第一个“L”表示从左向右扫描输入,第二个“L”表示产生最左推导,而“1”则表示在每一步中只需要向前看一个输入符号来决定语法分析动作。我们利用LL(1)的文法,可以构造出不需要回溯的递归下降语法分析器(即预测分析器)。
- 左递归文法和二义性文法都不可能是LL(1)的
对于任意两个不同的产生式:A→α | β,只有满足下面条件时,它们才是LL(1)文法:
1)、不存在终结符号a,使得 α 和 β 都能够推导出以 a 开头的串;
意思也就是说,FIRST(α) 和 FIRST(β) 是不相交的集合。
2)、 α和β中最多只有一个可以推导出空串;
当然这里一样的,FIRST(α) 和 FIRST(β) 是不相交的集合。如果出现了相交的集合,那么交集就是 ε 集。
3)、如果 β→*ϵ,那么 α 不能推导出任何以 FOLLOW(A) 中某个终结符号开头的串。类似的,对于 α 也一样;
这里我仔细的说一下,如果要推导出以FOLLOW(A)中某个终结符号开头的串,那也就是说 FIRST(α) 和 FOLLOW(A) 要存在交集。对于推导 β→*ϵ 而言,我们从第二点可以知道,那么此时 α 不能推导出 ε。这样看来要 FIRST(α) 和 FOLLOW(A) 存在交集,那是不可能发生的。