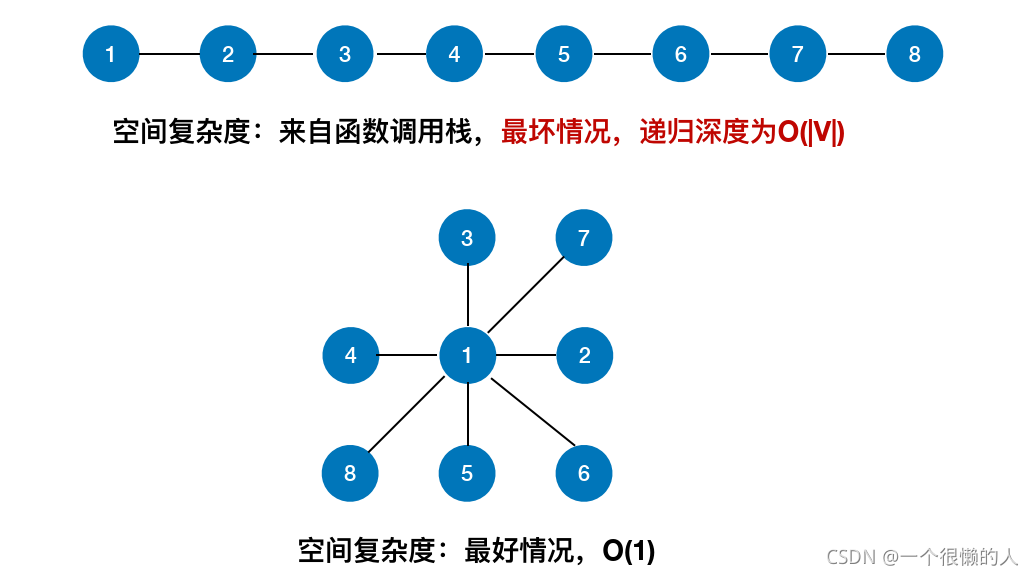
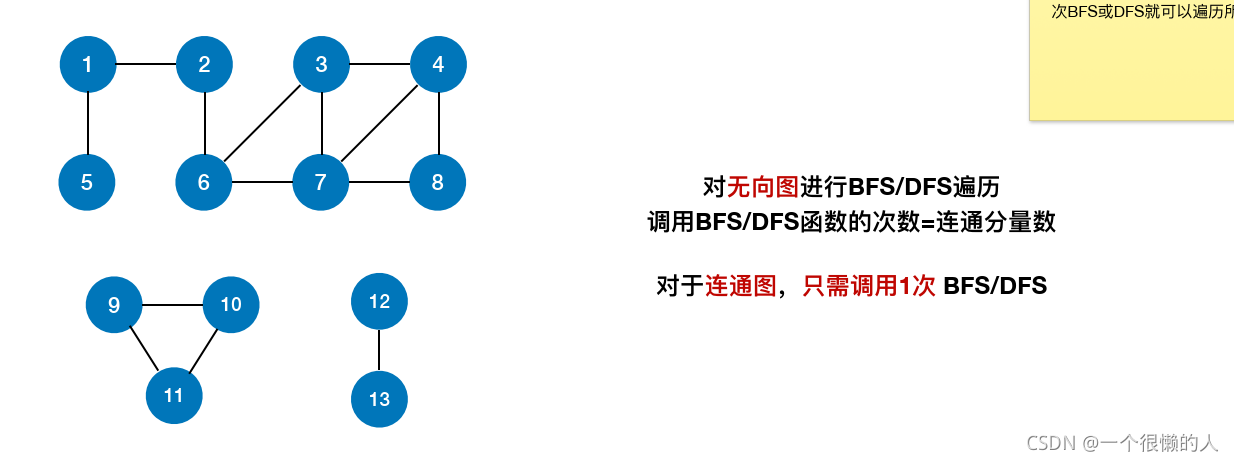
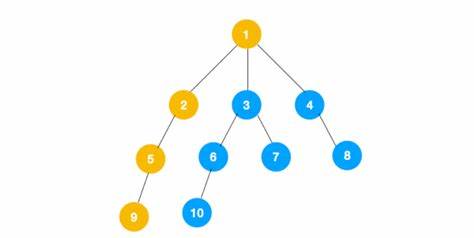
我的图床探索之旅:从踩坑到最优解前言搭建个人博客时,图床的选择让我走了不少弯路。经过几天的反复测试,我终于找到了一套稳定高效的解决方案。本文将详细介绍我的探索历程,希望能帮助到有同样需求的朋友。
一、云服务商方案体验1. 阿里云OSS使用体验:
上传速度:★★★★☆
访问速度:★★★★★
管理界面:★★★☆☆
痛点:
备案流程繁琐,耗时3天才完成,一般人不太容易拿到域名的备案,需要域名费用+对象存储费用+服务器费用,其中服务器费用太过巨大
费用计算复杂,一不小心就会超支
防盗链设置不够灵活
2. 腾讯云COS使用体验:
上传速度:★★★★★
访问速度:★★★★☆
管理界面:★★★★☆
痛点:
与阿里云类似需要备案
API文档不够友好
3.cloudfare R2存储总结
这个听说很好用,但是有一个致命缺点,你需要有信用卡或者PayPal账号
虽然国内的银联卡理论上也可以注册,但是国内的卡没有安全码,注册PayPal也有一定困难
二、成品图床深度评测1. SM.MS优点:
开箱即用
国内访问速度快
支持API调用
致命缺陷:
免费版5GB空间很快用完
图片管理功 ...
自我介绍大家好,非常开心,能够在这里和大家见面。
我再次希望向大家介绍一下我的个人代码托管平台,GitHub和gitee。
如果大家感兴趣,可以前往看看,希望能够对于你有所帮助
GitHubGitee
多重背包问题问题描述多重背包问题是一个经典的动态规划问题。在这个问题中,我们有 N 件物品,每件物品都有一个体积、一个价值和一个数量上限。我们的目标是将这些物品放入一个容量为 V 的背包中,使得背包中的物品总价值最大。
动态规划思路我们使用动态规划来解决这个问题。定义 dp[i][j] 表示前 i 件物品恰好放入一个容量为 j 的背包可以获得的最大价值。
状态转移方程状态转移方程为:
1dp[i][j] = max(dp[i-1][j], dp[i-1][j-k * wi] + k * vi)
其中 0 <= k <= si,wi 是第 i 件物品的体积,vi 是第 i 件物品的价值,si 是第 i 件物品的数量上限。
原始代码实现以下是原始的多重背包问题的代码实现:
123456789N, V = map(int, input().split())dp = [[0] * (V + 1) for _ in range(N + 1)]for i in range(1, N + 1): # 体积,价值,数量 wi, vi, si = map(int, input() ...
DFS剪枝简介DFS剪枝是一种启发式搜索算法,它通过对搜索树进行剪枝,来减少搜索树的大小,从而减少搜索时间。
DFS剪枝的基本思想是,在搜索树的每一步,都要判断是否可以直接跳过某些分支,从而减少搜索树的大小。
具体来说,DFS剪枝有以下几种方法:
剪枝准则:在搜索树的每一步,都要判断是否可以直接跳过某些分支,从而减少搜索树的大小。
启发式函数:启发式函数是指对节点的评估函数,它可以帮助搜索算法更好地选择下一步要探索的节点。
代价估计:代价估计是指估计节点的代价,并据此来判断是否应该继续探索该节点的子节点。
动态规划:动态规划是指利用搜索树的结构性质,对搜索树进行预处理,从而减少搜索树的大小。
启发式搜索:启发式搜索是指利用启发式函数对搜索树进行排序,从而减少搜索树的大小。
备忘录:备忘录是指在搜索树的每一步,都记录下已经探索过的节点,从而减少搜索树的大小。
并行搜索:并行搜索是指在多线程或多进程环境下,对搜索树进行搜索,从而减少搜索树的大小。
剪枝策略:剪枝策略是指对搜索树进行剪枝,从而减少搜索树的大小。
多目标搜索:多目标搜索是指在搜索树的每一步,都要同时考虑多个目 ...
回溯法求排列数123456789101112131415161718192021222324252627def dfs(depth): # depth: 当前深度 if depth == n: # 到达叶子节点,输出路径 print(path) return # 选择范围 for i in range(1, n+1): # 已经访问过的节点,跳过 if vis[i]: continue # 符合条件的节点,加入路径 vis[i] = True path.append(i) dfs(depth+1) # 回溯的时候,将当前节点从路径中移除 vis[i] = False path.pop(-1)n = int(input())vis = [False] * (n+1)path = []dfs(0)
回溯法求子集123456789101112131415161718n = ...
源文件声明规则
一个源文件中只能有一个 public 类
一个源文件中可以有多个非 public 类
源文件的名称应该和 public 类的类名保持一致。例如:源文件中 public 类的类名是 Employee,那么源文件应该命名为Employee.java。
示例1234567891011121314151617181920212223242526272829303132333435363738394041public class Puppy { private int age; private String name; // 构造器 public Puppy(String name) { this.name = name; System.out.println("小狗的名字是 : " + name); } // 设置 age 的值 public void setAge(int age) { this.age = age; &# ...
DFS基础DFS和n重循环模板123456789def dfs(depth): """ :param depth: 记录当前深度 :return """ if depth == N: # N重循环最内层执行的代码 return # 结束条件 # 每重循环进行的枚举选择
例题1. 打印相加为X的非严格递增n位序列1234567891011121314151617181920212223242526def dfs(depth, last_value): #depth:表示当前处于第depth层 #递归入口 if depth == n: #判断是否满足条件 if sum(path) != x: return print(path) return for i in range(last_value,x+1): path[depth] ...
电子计技术对于计算机发展的推动——以中央处理器(CPU)为例摘要:随着电子技术的不断创新和进步,计算机的性能和功能得到了进一步的发展。本文聚焦于计算机的中央处理器(CPU),通过阐述其随着电子技术发展而产生的变化历程,深入剖析电子技术对计算机硬件发展的推动作用,展现二者紧密的关联及电子技术的重要影响力。
关键词:电子技术,CPU,集成电路,芯片,算力,人工智能,机器学习,大数据
引言计算机作为现代社会不可或缺的工具,其性能的不断提升得益于硬件的持续发展。而在众多计算机硬件部件中,中央处理器(CPU)无疑起着核心作用,它的发展演变与电子技术的进步息息相关,电子技术的每一次突破都为 CPU 的性能提升带来了新的契机。其中,也诞生了计算机历史上比较著名的定理,如摩尔定理,即每过 18 个月,中央处理器(CPU)的价格下降一半,性能提高一倍。
正文电子技术发展初期和早期 CPU在电子技术发展的早期阶段,那时主要采用电子管技术。世界上第一台通用计算机 ENIAC 便是以电子管作为基础元件构建其 CPU 等部件的。电子管体积庞大、能耗极高且容易损坏,这使得当时的 CPU 运算速度慢、处理能力有限, ...
Welcome to Hexo! This is my very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.
Quick StartCreate a new post1$ hexo new "My New Post"
More info: Writing
Run server1$ hexo server
More info: Server
Generate static files1$ hexo generate
More info: Generating
Deploy to remote sites1$ hexo deploy
More info: Deployment